Kabsch Algorithm
Usage / Example
using BiomolecularStructures.Kabsch
# Define two matrices P, Q:
P = [-1. 0. 0.; 0. 0. 0.; 0. 1. 0.; 0. 1. 1]
Q = [0. -1. -1.; 0. -1. 0; 0. 0. 0.; -1. 0. 0.]
RMSD before superimposing:
julia> rmsd(P, Q)
1.4142135623730951
After running the Kabsch algorithm:
julia> kabsch_rmsd(P, Q)
2.435541875787129e-16
Exported functions
rmsd
rmsd(A::Array{Float64,2}, B::Array{Float64,2})
Calculates the root mean square deviation of two matrices A and B in using the following formula (Kavraki, L. 2007):
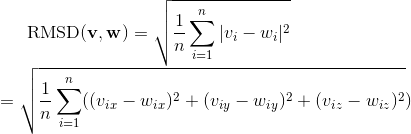
A a matrix
B a matrix
calc_centroid
calc_centroid(m::Array{Float64,2})
Returns the centroid of a matrix m as a [x y z] vector (An Array{Float54,2}).
m a matrix
translate_points
translate_points(P::Array{Float64,2}, Q::Array{Float64,2})
Translates two matrices P, Q so that their centroids are equal to the origin of the coordinate system.
P a matrix
Q a matrix
kabsch
kabsch(reference::Array{Float64,2},coords::Array{Float64,2})
Calculates the optimal rotation matrix of two matrices P, Q and superimposes the two matrices
reference a matrix to superimpose on.
coords the matrix to be rotated
Using translate_points it shifts the matrices' centroids to the origin of the coordinate system, then computes the covariance matrix A:
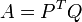
Next is the singular value decomposition of A:
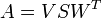
It's possible that the rotation matrix needs correction:
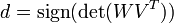
The optimal rotation matrix U is calculated:
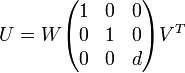
The last two steps are translating U so that the superimposed matrix will "fit" to the reference matrix and then performing the rotation and shifting it to the origin of the coordinate system.
The function returns the superimposed matrix.
kabsch_rmsd
kabsch_rmsd(P::Array{Float64,2}, Q::Array{Float64,2})
Directly returns the RMSD after rotation for convenience.
P reference matrix
Q matrix to be rotated
Background
The Kabsch algorithm (Kabsch 1976, Kabsch 1978), solves a constrained orthogonal Procrustes problem. In Greek mythology Procrustes, ("the stretcher") is a son of Poseidon who invited travelers to his home and then stretched (or amputated limbs in later versions) to fit his guests to an iron bed using his smith's hammer.
A Procrustes problem is to compare two (or more) shapes. For this, they must be optimally superimposed by translating, rotating and scaling them.
The constraint applied is that only rotations of the shapes (or matrices in this case) are allowed. Additionally, reflections are not allowed.
In Bioinformatics this applies to superimposing the Cα atomic coordinates of two protein structures so that the RMSD (Root mean squared deviation), one of the most commonly used difference measures (Kavraki, L. 2007), is minimal.
To illustrate this, the following excerpt of the PDB file of human deoxyhaemoglobin shows part of one of the alpha chains of the structure. The Cα atomic coordinates shown can be used to construct a reference matrix which together with another matrix of coordinates (constructed the same way) could serve as the input of the algorithm.
ATOM 17 CA SER A 3 12.286 19.774 7.034 1.00 27.60 C
ATOM 18 C SER A 3 13.529 20.322 6.334 1.00 30.36 C
ATOM 19 O SER A 3 13.995 19.754 5.344 1.00 27.40 O
ATOM 20 CB SER A 3 12.719 19.060 8.326 1.00 23.83 C
ATOM 21 OG SER A 3 13.844 18.245 8.107 1.00 29.07 O
ATOM 22 N PRO A 4 14.075 21.454 6.786 1.00 37.36 N
ATOM 23 CA PRO A 4 15.285 22.042 6.167 1.00 39.58 C
ATOM 24 C PRO A 4 16.466 21.103 6.290 1.00 21.30 C
ATOM 25 O PRO A 4 17.288 21.019 5.368 1.00 32.82 O
ATOM 26 CB PRO A 4 15.637 23.315 6.942 1.00 45.84 C
ATOM 27 CG PRO A 4 14.398 23.603 7.765 1.00 43.31 C
ATOM 28 CD PRO A 4 13.513 22.346 7.796 1.00 38.50 C
ATOM 29 N ALA A 5 16.484 20.391 7.438 1.00 22.62 N
ATOM 30 CA ALA A 5 17.533 19.415 7.651 1.00 26.71 C
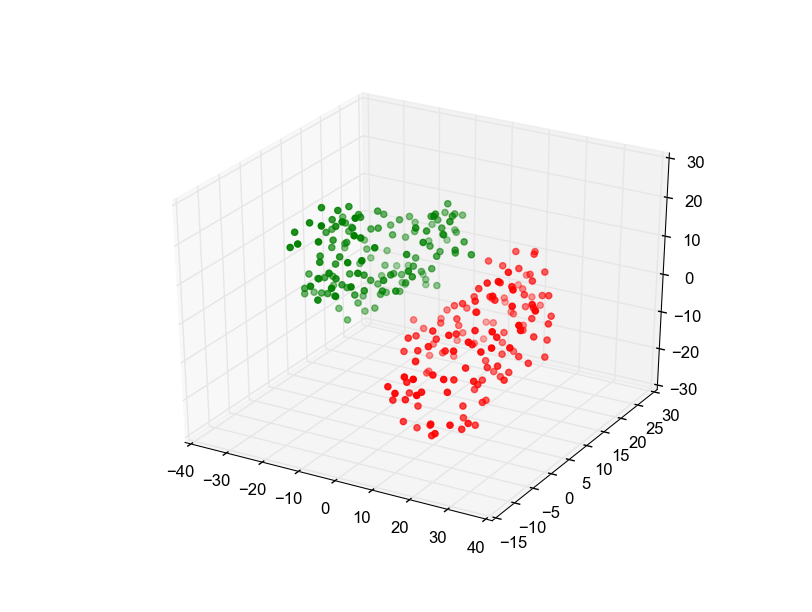
Plotting the initial coordinates of both alpha chains (shown in red and green) already hints at a non-minimal RMSD (39.46851976701876 Å).
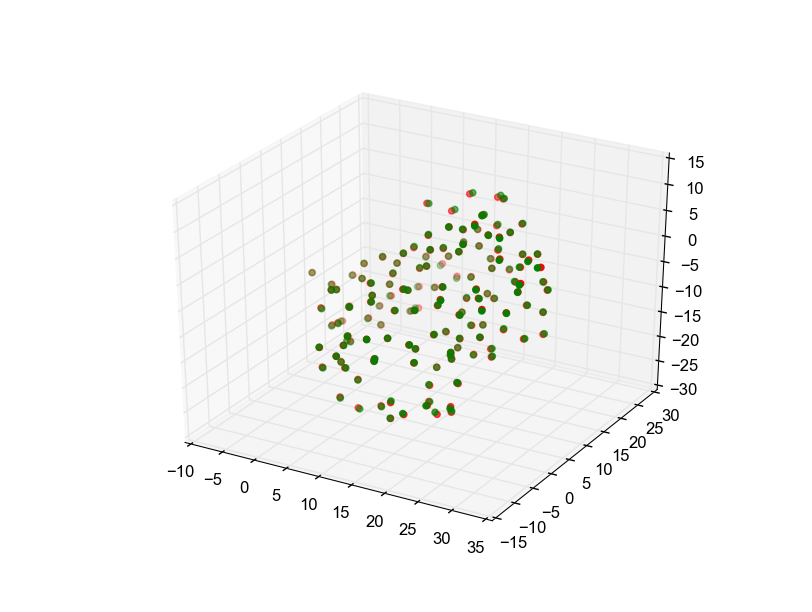
After running the algorithm the alpha chains are superimposed and the RMSD is minimized (0.2300387105661853 Å).
References
Kavraki, L. Molecular Distance Measures. OpenStax CNX. 11. Juni 2007